Level 1 CFA® Exam:
T-Distribution, Chi-Square Distribution, F-Distribution
Student's t-distribution (aka. t-distribution) is a symmetrical, bell-shaped probability distribution described by only one parameter called degrees of freedom (df). T-distribution is used for the construction of confidence intervals and hypothesis testing if the sample is small, namely lower than 30 observations.
The concept of degrees of freedom (df) is present in many important distributions. It is a number of independent observations used to estimate a statistic. In the case of a confidence interval, the number of degrees of freedom is equal to sample size minus 1.
The t-distribution is symmetric and bell-shaped, like the normal distribution. It is fully described by degrees of freedom. There is a different t-distribution for each number of degrees of freedom. Compared to the normal distribution, the t-distribution is flatter around the mean and has fatter tails. The mean of the t-distribution is zero, as in the case of the standardized normal distribution and the variance for the numbers of degrees of freedom greater than 2 is equal to:
\(\text{variance t-distribution}=\frac{df}{df-2}\)
(...)
A chi-square distribution:
- is defined by one parameter, namely the number of degrees of freedom,
- is asymmetrical, and
- is bounded below by zero.
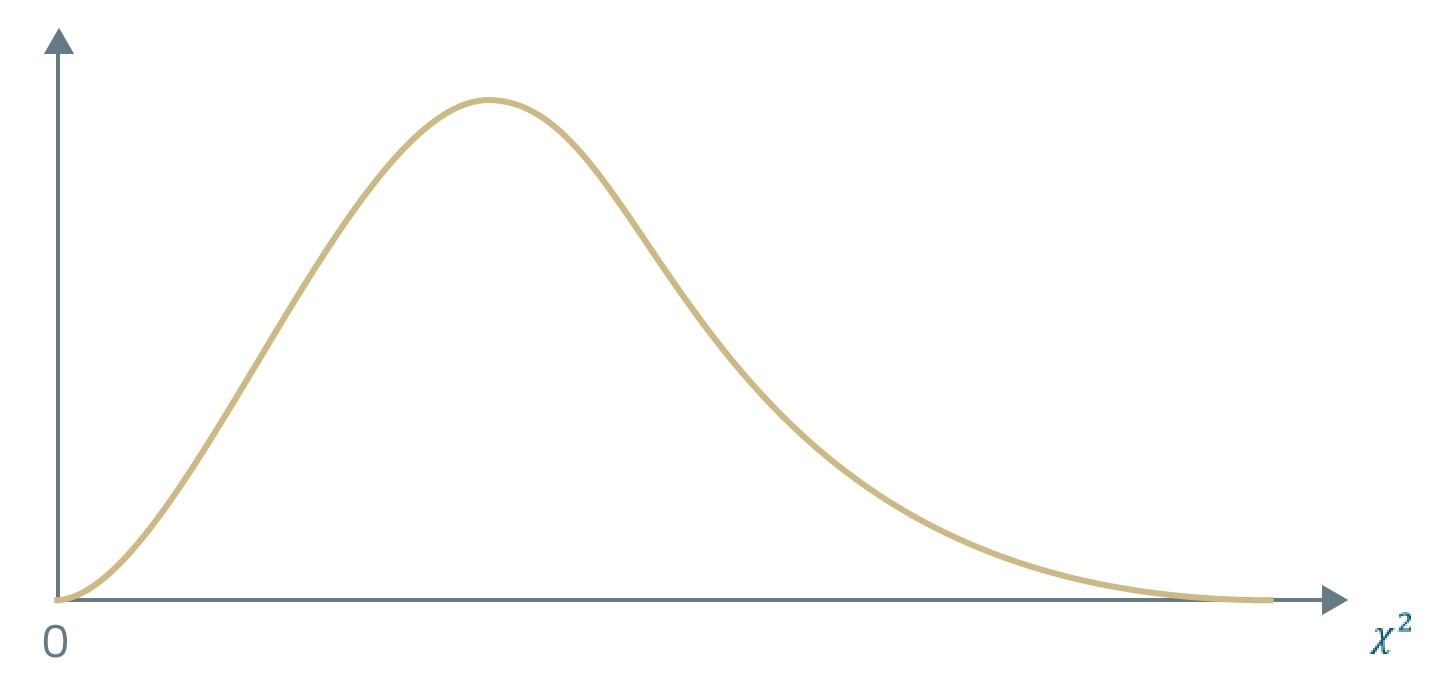
We use a chi-square test statistic in tests concerning a single variance of a normally distributed population.
Because a chi-square distribution does not take on negative values, the chi-square test is a good test for variance, because variance is always greater than or equal to zero.
As in the case of the t-test concerning a single mean, the number of degrees of freedom is equal to the sample size minus 1.
Like the chi-square distribution, the F-distribution is a family of asymmetrical distributions bounded from below by 0. Each F-distribution is defined by two values of degrees of freedom, called the numerator and denominator degrees of freedom.
We can use F-distribution for tests concerning the equality or inequality of two variances of normally distributed populations.
Assuming that the samples drew from these two populations are independent, we can test them with an F-test. The F-test is the ratio of sample variances.
While conducting the F-test, we have to compute the sample variances for both populations. Note that we put the greater variance in the numerator and the lower one in the denominator.
Level 1 CFA Exam Takeaways: Student’s T-Distribution, Chi-Square Distribution, & F-Distribution
star content check off when done- Student’s T-distribution is defined by only one parameter called degrees of freedom.
- The higher the number of degrees of freedom and, as a consequence, the higher the sample size, the more the t-distribution resembles the normal distribution.
- A chi-square distribution is defined by one parameter, namely the number of degrees of freedom. It is asymmetrical and bounded below by zero.
- We use a chi-square test statistic in tests concerning a single variance of a normally distributed population.
- Like the chi-square distribution, the F-distribution is a family of asymmetrical distributions bounded from below by 0. Each F-distribution is defined by two values of degrees of freedom, called the numerator and denominator degrees of freedom.

