Level 1 CFA® Exam:
Binomial Distribution and Bernoulli Trial
Quite frequently, we are interested in random variables that can take on only two outcomes. Usually, one of the outcomes is called a success and the other one – a failure. The random variable that can take on only two outcomes is called a Bernoulli random variable. (Bernoulli was a mathematician that lived in the 17th century.)
One example of a Bernoulli random variable would be an outcome of tossing a coin because a coin comes up with either heads or tails when it is tossed. So, suppose that we decide to toss the coin and if it comes up heads it is a success, and if tails – it is a failure. Of course, we might as well consider tails to be a success – it’s all up to us. If in our trial we use a fair coin, the probability of success and failure would be the same and equal to 0.5. By the way, \(p\) – that is the probability of success – is the only parameter of Bernoulli distribution.
The Bernoulli random variable found application in what we call the binomial tree, a tool useful for determining movements of financial instrument prices. The binomial tree constitutes the basis of the binomial option pricing model, or the binomial model for short. The model is also called the Cox-Ross-Rubinstein model after its originators.
But how exactly does a binomial tree look like? Have a look at the figure exemplifying a simple binomial tree, called one-period binomial tree:
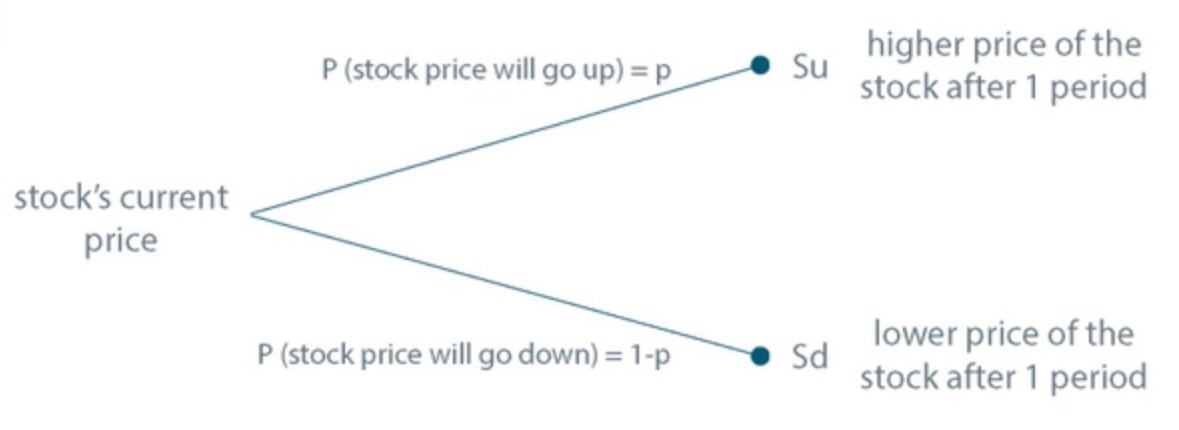
As we have already mentioned, a binomial tree can be used for estimating possible future prices of financial instruments and their probabilities. Using a binomial tree, we assume that the price of a stock can change only once at a certain point in time, for example, every day or every month. Then we consider two possible scenarios, that is the price can either increase or decrease in a given period.
If we know today’s price of a stock and the probabilities that the price either goes up or down in the next period, we can easily learn about possible future prices of the stock and find out how probable they are. We can also determine the value of any option either American or European for which the stock is the underlying asset.
If you don’t know yet what options are or what an American or a European option is, don’t worry – you will learn a lot about options from our study content on derivative investments. As for now, it suffices if you know that an option is a type of a derivative, and a derivative is a financial instrument whose value depends on the value of some underlying asset, for example, a stock.
The price of a stock today is USD 100 and the probability that the stock price will rise in the next period equals 0.7. Using a two-period binomial tree and assuming that in one period the price can either go up or decrease by 5%, calculate possible future prices of the stock at the end of the second period and the corresponding probabilities.
(...)
Our discussion of variables with two possible outcomes leads us to the Bernoulli trial.
A Bernoulli trial is a sequence of identical tests that meet the following conditions:
- There are two possible outcomes, that we call success and failure, which are mutually exclusive and complementary.
- The probability of success, denoted as \(p\), is the same for each trial. The probability of failure is denoted as \(q\), and \(q=1-p\).
- The outcome of a trial doesn’t affect the outcome of any other trial. In other words, Bernoulli trials are independent of each other.
An example of a Bernoulli trial: flipping a coin
The number of successes in a sequence of \(n\) Bernoulli trials is called a binomial random variable. In other words, a binomial random variable is a random variable X, that is the number of successes in a sequence of \(n\) Bernoulli trials.
A binomial random variable is the sum of Bernoulli random variables. As we mentioned before, a Bernoulli random variable equals 1 if the outcome of a single trial is a success, and 0 in the case of a failure. If there are \(n\) Bernoulli trials, and X is a binomial random variable, and Ys are Bernoulli random variables (taking values 1 or 0 depending on the success of trials), then:
\(X=Y_1+Y_2+...+Y_{n-1}+Y_N\)
An example of a binomial random variable outcome: we get 4 heads when we flip a coin 10 times
(...)
Let the binomial random variable be denoted as X, and let heads be success denoted as \(p\). Suppose that we toss the coin 6 times. What are the parameters of the binomial distribution?
The variable X has a binomial distribution with parameters:
- \(n=6\) and
- \(p=0.5\).
What's the probability that in 6 tosses the coin will come up:
- heads, 3 times
- heads, 5 times
- heads, 1 or 3 times
- heads, up to 3 times
(...)
Mean:
In the case of a single trial: \(\text{mean}=p\).
If there are \(n\) trials: \(\text{mean}=n\times{p}\).
Note that the mean is simply the expected value of a random variable in a given distribution. When the probability of an event equals 0.5, the binomial distribution is symmetrical. This is the case in the example with six tosses of a coin.
Variance:
In the case of a single trial: \(\text{variance}=p\times{(1-p)}\).
If there are \(n\) trials: \(\text{variance}=n\times{p}\times{(1-p)}\).
Calculate the mean and the variance of a binomial random variable assuming we tossed a coin 6 times.
If there are \(6\) trials:
\(\text{mean}=n\times{p}=6\times0.5=3\).
\(\text{variance}=n\times{p}\times{1-p}=6\times0.5\times0.5=1.5\).
Level 1 CFA Exam Takeaways: Binomial Distribution and Bernoulli Trial
star content check off when done- The random variable that can take on only two outcomes is called a Bernoulli random variable.
- The binomial tree constitutes the basis of the binomial option pricing model.
- A Bernoulli trial is a sequence of identical tests that meet the following conditions: (1) There are two possible outcomes (aka. success and failure) which are mutually exclusive and complementary; (2) The probability of success, is the same for each trial; (3) The outcome of a trial does not affect the outcome of any other trial.
- The number of successes in a sequence of \(n\) Bernoulli trials is called a binomial random variable.
- A binomial random variable is the sum of Bernoulli random variables.
- A binomial distribution is a distribution obtained in a number of Bernoulli trials.
- When the probability of an event equals 0.5, the binomial distribution is symmetrical.


