Level 1 CFA® Exam:
Introduction to Bond Valuation
As we know, the price of a well-priced bond is equal to the present value of the future cash flows from the bond, namely coupons, and the bond’s par value. Thus, to determine the price of the bond, we must know the value of the cash flows from the bond and the value of the discount rate used to discount the cash flows.
The value of the discount rate depends on the risk associated with the bond’s cash flows. Therefore, if we have two bonds with different credit ratings, we should apply the higher discount rate when valuing the bond with the lower rating, that is the more risky bond, and the lower discount rate when valuing the less risky one.
Generally, we have at our disposal four methods of bond valuation. Each of them is based on the time value of money concept. What distinguishes these methods is the applied discount rate. We can value a bond using:
- a market discount rate,
- spot rates and forward rates,
- binomial interest rate trees, or
- matrix pricing.
CFA Exam: Market Discount Rate
The first method to be used in your level 1 CFA exam is the simplest one. It assumes using only one discount rate for the entire period from today to the maturity date.
In other words, each of the bond’s future cash flows is discounted using the same discount rate. This discount rate is called a market discount rate or a required rate of return or simply a required yield. We will discuss this method in greater detail in the next lesson.
The second method assumes the use of a set of spot rates (or forward rates), to discount the cash flows from the bond.
We can say that the spot rate is the rate applicable to the period from today to some point in time in the future, and the forward rate is the interest rate applicable to two periods in the future.
Spot rates for different periods usually differ from each other. For example, the value of a spot rate for the period from today to the end of the first year is usually different than for example the value of the spot rate for the period from today to the end of the second year. The same holds for forward rates. For example, the forward rate for the period from the third to the fourth year will be different than the forward rate for the period from the fifth to the sixth year.
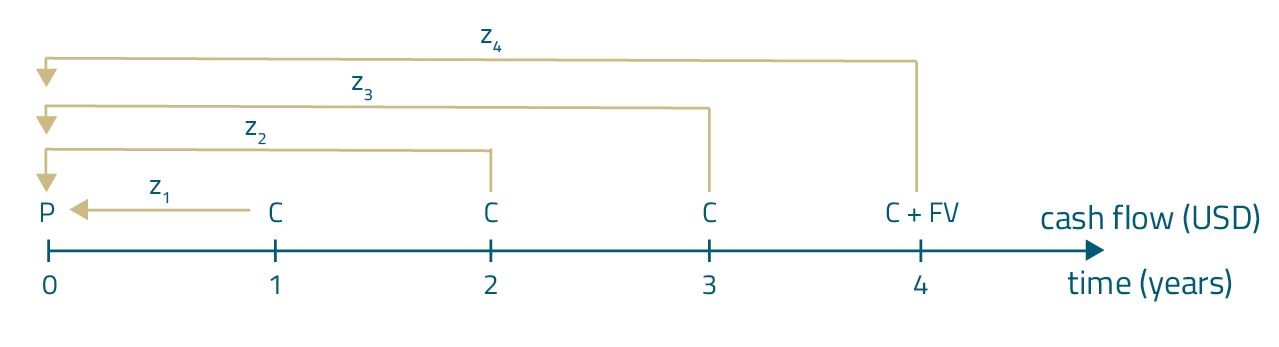
Back to the valuation of bonds. In the case of bond valuation based on spot rates, each of the bond’s cash flows will be discounted by a different spot rate applicable to the given cash flow. For example, for a 4-year bond, the first coupon payment will be discounted using spot rate \(z_1\), the second coupon payment will be discounted using spot rate \(z_2\), the coupon at the end of the third year will be discounted using spot rate \(z_3\), and the last coupon plus the par value of the bond will be discounted with the aid of spot rate \(z_4\). For comparison, in the first method (market discount rate) we will use the same discount rate for every cash flow.
(...)
The fourth method of valuing bonds, namely matrix pricing, is a variation of the first method.
In the first method, we assumed that the discount rate is known. Under the matrix pricing method, it is assumed that we do not know the discount rate at the beginning. We use matrix pricing to determine it.
To compute the discount rate, we use the linear interpolation and yields to maturity of similar bonds. Similar means for example with similar risk, but different maturity dates. We will use matrix pricing either when the bond valued is illiquid or when we intend to value the bond that is to be issued shortly.
- The price of a well-priced bond is equal to the present value of the future cash flows from the bond, namely coupons, and the bond’s par value.
- We can value a bond using: (1) a market discount rate, (2) spot rates and forward rates, (3) binomial interest rate trees, or (4) matrix pricing.
- The bond valuation method applying a market discount rate assumes using only one discount rate for the entire period from today to the maturity date.
- A spot rate is the rate applicable to the period from today to some point in time in the future and a forward rate is the interest rate applicable to two periods in the future.
- The bond valuation method that applies binomial interest rate trees assumes that interest rates are volatile.
- In matrix pricing, to compute the discount rate, we use the linear interpolation and yields to maturity of similar bonds.
- We will use matrix pricing either when the bond valued is illiquid or when we intend to value the bond that is to be issued shortly.


