Level 1 CFA® Exam:
CAL, CML & Market Portfolio
In one of the previous lessons, we introduced the term of the capital allocation line (CAL). Remember that this line connects risky assets with the risk-free asset. In the graph representing the risk and return relationship, it is a straight line. It is the risky assets part of the portfolio that mostly determines the expected risk and return of the portfolio.
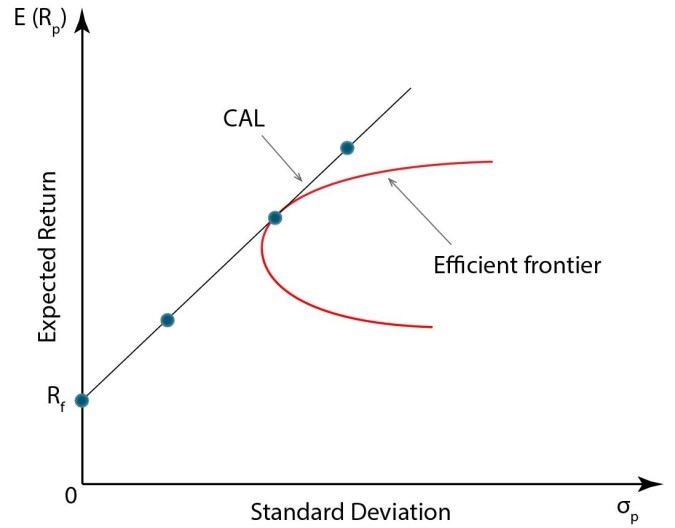
Usually, it’s not a problem to set a risk-free rate of return as typically the point of reference is the T-bill yield. However, determining the rate of return and risk of the portfolio of risky assets is, in fact, quite difficult. Markets aren't perfect and different investors find different ways to estimate the expected rate of return and risk and to find correlations between assets. That's why every investor may put the efficient frontier in a different place and consequently do the same with the capital allocation line.
Another cause of different capital allocation lines obtained by different investors is the fact that not every investor has access to all kinds of assets, for example, because of political, legal, or technological reasons. Such factors also largely affect how investors build their optimal portfolios of risky assets. It should be kept in mind that the capital allocation line refers to an individual investor and it is the most profitable for him only.
As you can see, in the case of divergent expectations of investors, it would be difficult to create one optimal portfolio for all investors. That's why Modern Portfolio Theory applies the concept of homogeneous expectations. It is assumed that all investors obtain the same estimates of the expected return on an investment, its risk, and of the correlations between the assets, which makes a portfolio analysis easier. Consequently, all investors come up with the same effective frontier, the same capital allocation line, and the same optimal risky portfolio.
Because of the homogeneity of expectations all investors should invest in the same portfolio of risky assets. If all investors invest in the same portfolio, such a portfolio will include all assets available in the market, and – because of this – it is referred to as a market portfolio.
(...)
The assumption of homogeneity of expectations has allowed us to select one optimal risky portfolio and construct one capital allocation line for all investors. If all investors evaluate assets in the same way, then each of them will want to have the same optimal risky portfolio.
The capital market line is a special kind of the capital allocation line where an optimal risky portfolio is the market portfolio. And so, even though capital allocation lines may vary for different investors, the capital market line is the same for each of them and it takes this form:
The CML has a positive slope and it takes the form:
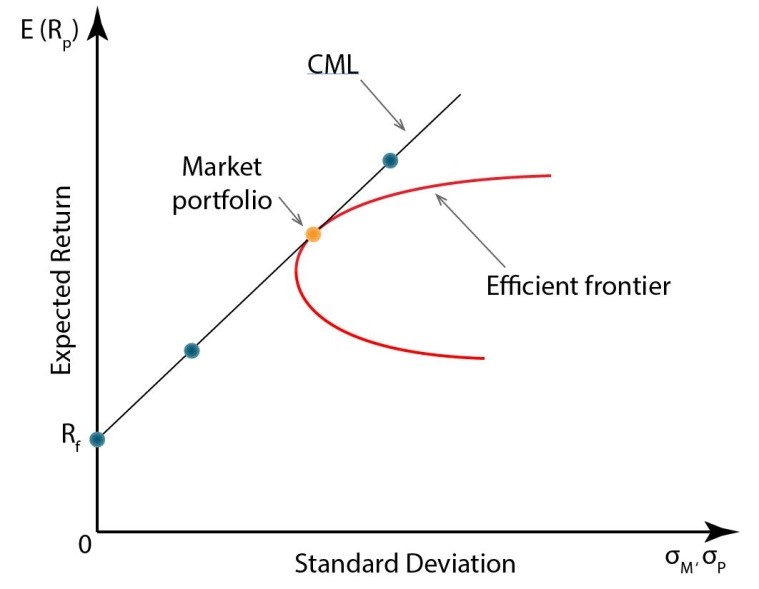
If the risk of our portfolio that is measured by its standard deviation is to be zero, then the rate of return on the portfolio equals the risk-free rate of return.
The expected return on the market portfolio minus risk-free return is called the market risk premium. The market risk premium shows how much excess return over the risk-free return can be assigned to one unit of market risk.
As in the case of the capital allocation line, an investor may freely move along the capital market line and he may select the portfolio that gives him the greatest utility out of all effective portfolios that lie on the CML.
If the portfolio selected by the investor consists of risk-free assets only and doesn’t include the market portfolio, the return on the investment will be equal to the risk-free return.
When an investor constructs a portfolio that includes risk-free assets and the market portfolio, both the rate of return and the risk will be proportionate to the shares of the risk-free assets and the market portfolio. The bigger the share of the market portfolio as compared to the share of risk-free assets, the higher the expected risk and return of the selected portfolio.
(...)
Let's assume that the risk-free rate is 4% and the return on the market portfolio is estimated at 12% with a standard deviation of 15%. What's the risk and the composition of the portfolio with the rate of return of 10%?
(...)
Before we end, we're going to say a few words about informationally efficient markets. If markets were informationally efficient, then the prices of assets would adequately reflect their real value and investors would have equal access to information. Therefore, any available information, e.g. on a particular enterprise, would be immediately reflected in the stock price. So it would be impossible for any investor to use any piece of information to beat the market.
The investors who assume information efficiency usually invest in a market portfolio (for example an index) because they do not believe that they can beat the market. The strategy used by those market participants is called a passive investment strategy.
However, most investors or fund managers assume that the market is not fully effective and they try to find underestimated or overestimated assets that they buy or sell, respectively. Such a strategy is called active investment management.
- Due to the homogeneity of expectations all investors should invest in the same portfolio of risky assets, called a market portfolio.
- In the market portfolio, the weights of individual assets are equal to the percentage share of those assets in the total market value of all assets.
- The capital market line is a special kind of the capital allocation line where an optimal risky portfolio is the market portfolio.
- When an investor constructs a portfolio that includes risk-free assets and the market portfolio, both the rate of return and the risk will be proportionate to the shares of the risk-free assets and the market portfolio.
- If markets were informationally efficient, then the prices of assets would adequately reflect their real value and investors would have equal access to information.


