Level 1 CFA® Exam:
Duration & Convexity - Introduction
The bond price changes in the opposite direction to changes in the yield-to-maturity. So, if the yield-to-maturity rises, the bond price falls and if the yield-to-maturity decreases, the bond price increases.
The risk associated with a fall in the bond price due to an increase in interest rates is called the interest rate risk.
A small side note here. Some people use the term “interest rate risk” to describe the risk associated with both the increase and decrease in the yield-to-maturity. As the result, they divide interest-rate risk into:
- the coupon reinvestment risk, and
- the market price risk.
The coupon reinvestment risk is when yields decrease, and the market price risk is when yields increase.
However, no matter whether we distinguish different types of risks or not, the key thing here is to understand why the interest rate risk occurs.
Look at the graph:
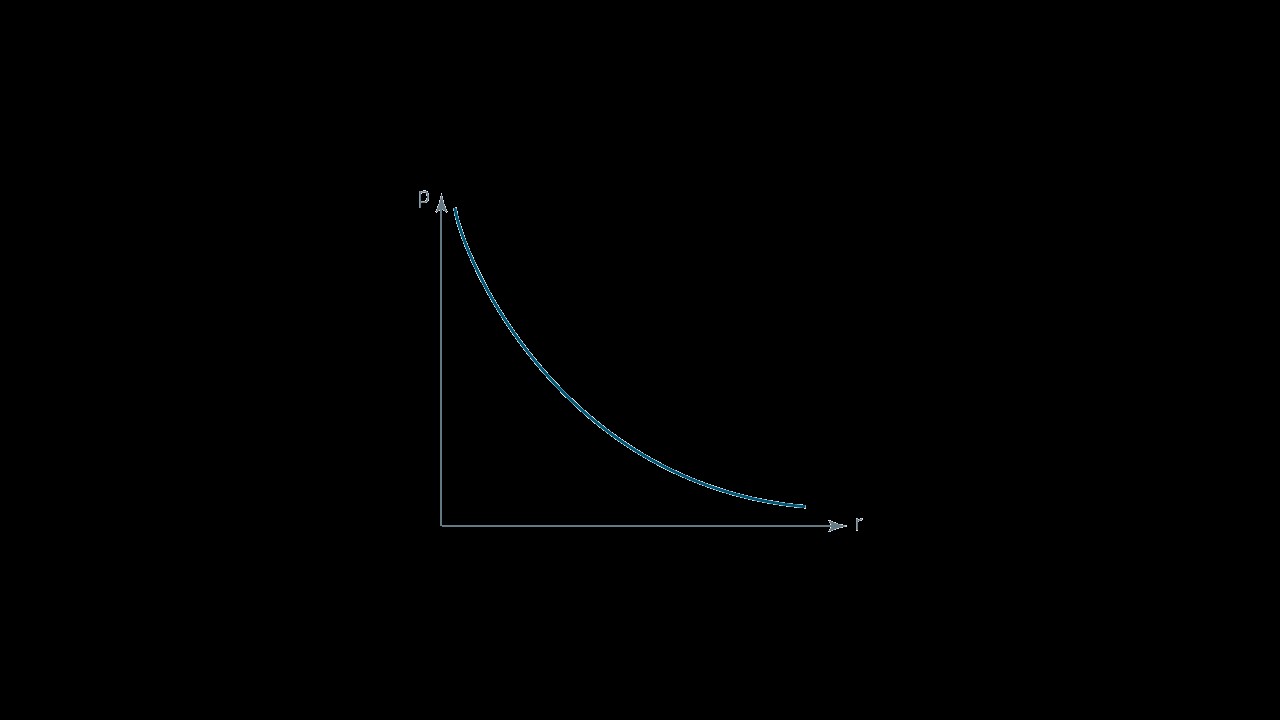
As you can see, the relationship between the bond price and the yield-to-maturity is not linear and the curve is convex. There are two consequences of this:
- Firstly, if the yield-to-maturity changes only a bit, namely it either increases or decreases a bit, the absolute value of the percentage change in the bond price will be the same both for the increase and decrease in the yield-to-maturity. Of course, if the yield-to-maturity increases, the price of the bond will decrease and vice versa.
- Secondly, if the yield-to-maturity changes a lot, the absolute value of the percentage change in the bond price will be lower if the yield-to-maturity increases, than if the yield-to-maturity decreases. This is the result of the convexity of the curve. It means that if the yield-to-maturity changes a lot, the bond price will increase more as the result of a decrease in the required rate of return than it will decrease as the result of an increase in the yield-to-maturity.
These consequences have a great impact on the interest rate risk measurement. If we assume that the yield-to-maturity will change only a bit, we can use duration alone to measure the interest rate risk. However, if we assume that the yield-to-maturity will change a lot, we have to use both duration and convexity and adjust the results obtained with the aid of the former measure using the so-called convexity adjustment.
Duration measures price sensitivity to changes in interest rates. There are different types of duration statistics. We distinguish:
- Macaulay duration,
- approximate Macaulay duration,
- modified duration,
- approximate modified duration,
- money duration,
- price value of a basis point, and
- effective duration.
In this lesson, we will focus on Macaulay duration and modified duration.
Macaulay Duration
Below you can see the general formula for Macaulay duration to be used in your level 1 CFA exam:
Note:
The denominator of the formula is simply the bond price:
Also for a bond that has just paid its coupon, \(t=0\), so the formula simplifies a bit.
Let’s rewrite the basic formula to gain a better understanding of how we can interpret it:
\(1-t/T\), \(2-t/T\) and so on until \(N-t/T\) are periods of time remaining until consecutive coupons.
\(\frac{C}{(1+r)^{1-t/T}}\) and so on are present values of the bond’s cash flows. Note that the sum of present values of the bond’s cash flows is equal to the price of the bond.
So, we can say that the Macaulay duration is the weighted average of coupon periods (for example years) where a given weight equals the present value of the bond’s cash flow that occurs at the end of the given period divided by the bond price. That is why we often say that the Macaulay duration equals X YEARS, for example, 5.2 years.
The Macaulay duration can be interpreted as:
- the number of years that an investor has to wait until the investment pays back assuming that the yield doesn’t change,
- a measure of the interest rate risk.
What is the Macaulay duration of the annual coupon bond with a 2% coupon rate and the price equal to USD 75.9817? Assume that the maturity of the bond equals 3 years.
(...)
The par value and the price of a five-year zero-coupon bond equals USD 100 and USD 89, respectively. What is the value of the Macaulay duration for the bond assuming periodicity of 1?
(...)
The other concept we will learn about today is the modified duration:
What is the modified duration of the annual coupon bond with a 2% coupon rate, the price equal to USD 75.9817, and a maturity of 3 years if the Macaulay duration is equal to 2.932?
(...)
Note that because the yield-to-maturity is always greater than 0, the modified duration is always lower than the Macaulay duration.
So, we know how to compute the Macaulay duration, we know how to compute the Modified duration, but why should we even bother to compute them?
The reason is simple:
We can use the modified duration to compute the percentage price change for a bond assuming a change in the yield. In other words, we can use duration to measure the interest rate risk. Have a look at the formula:
If the yield for a bond whose modified duration equals 4.5 rises from 5.2% to 5.5%, how much will the price of the bond change?
(...)
If the yield for a bond whose modified duration equals 4.5 decreases from 5.2% to 4.9%, how much will the price of the bond change?
(...)
Have a look at the formula once again:
There is a minus sign before ModD because the bond price moves in the direction opposite to that of the yield, namely if the yield increases, the bond price will decrease, and if the yield decreases, the bond price will increase.
What else can we notice?
The greater the modified duration, the greater the percentage price change, and vice versa. The lower the modified duration, the lower the percentage price change.
Also:
The greater the yield change, the greater the percentage price change, and the lower the yield change, the lower the percentage price change.
Additionally, you should note that the formula in this form has 2 major drawbacks:
- First of all, the formula for the percentage change of the bond price gives only approximate results.
- Secondly, as you can see in Examples 4 and 5, when the yield changed by the same value but in the opposite direction, the bond price changed by exactly the same amount but in the opposite direction. As we said at the beginning of this lesson, it is not the case. If the yield-to-maturity changes a lot, the absolute value of the percentage change in the bond price will be lower if the yield-to-maturity increases, than if the yield-to-maturity decreases.
To analyze the concept of the modified duration, have a look at the graph:
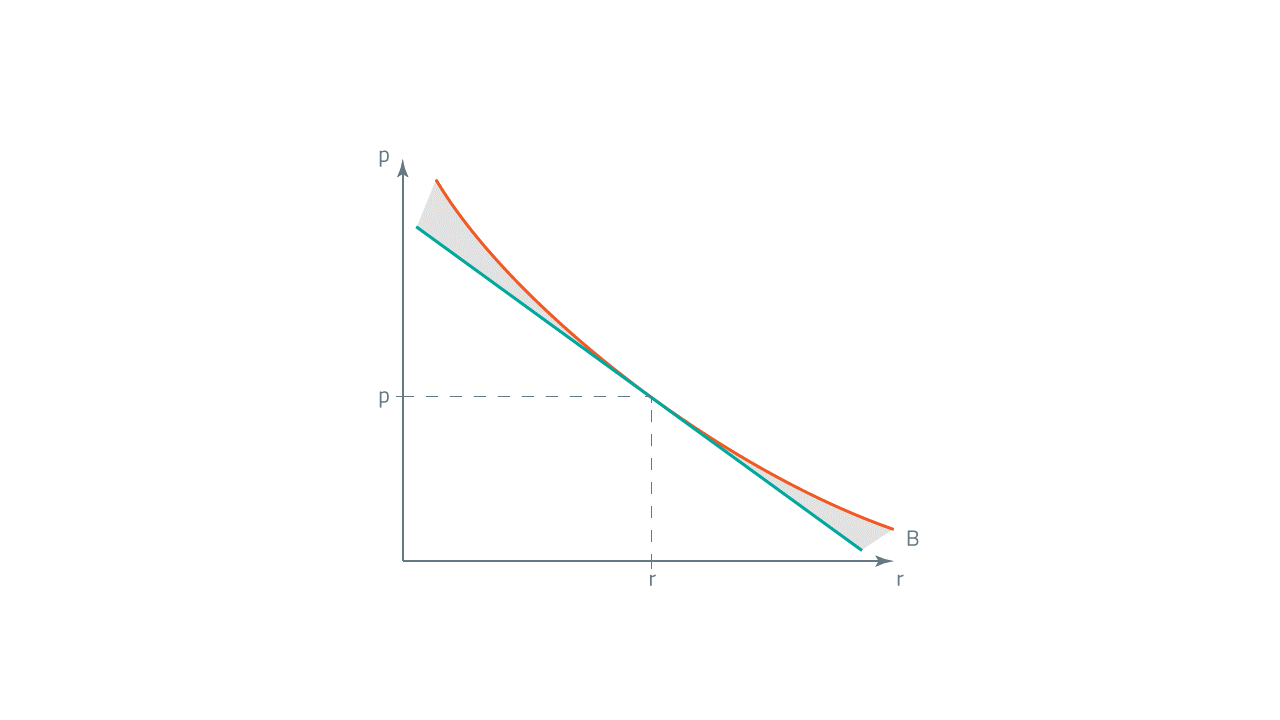
P stands for the current price and r is the current yield-to-maturity. The green line indicates what will be the new price of the bond if the interest rate changes and if we use the formula incorporating the modified duration. Note, however, that the green line is straight and the curve (the red line) showing the relationship between the price and yield is convex.
If the change in the yield is very small and if we use the formula incorporating the modified duration only, we will get almost precise results. However, as you can see in the graph if the change in the yield is big, the result obtained using the formula differs a lot from the real result. That is why we need to introduce the concept of convexity to be able to accurately measure the interest rate risk of the bond.
- The higher the duration, the more the bond price changes due to changes in the yield. This means that the higher the duration, the higher the bond interest rate risk. And vice versa. The lower the duration, the less the bond price changes due to changes in the yield and the lower the bond interest rate risk is.
- The duration differs for bonds with different coupons.
- For all bonds without embedded options, the Macaulay duration is lower than time to maturity except for zero-coupon bonds.
- A zero-coupon bond has the Macaulay duration equal to its time to maturity.
- Since the modified duration is always lower than the Macaulay duration, all bonds without embedded options have modified durations lower than their times to maturity.
- The lower the ratio of the coupon to the par value, the greater the duration and the greater the interest rate risk. So, a zero-coupon bond has the greatest interest rate risk from all bonds with the same maturity and the same credit rating.
- The modified duration of a consol, which is also called perpetuity, is always equal to 1 divided by yield-to-maturity.
- For floaters, duration does not exceed the period to the next coupon payment. So, the interest rate risk associated with these bonds is small.
- The duration changes in time.
- The duration of all bonds approaches 0 when the maturity date gets near. The only exception are long-term discount bonds. For this type of bonds, if the term to maturity is long enough, the duration increases as the bond approaches the maturity date.
- Usually between coupon payments, the duration decrease in a linear manner. After the coupon is paid, the duration increases suddenly and then starts to decrease once again. And so on.
- Modified duration depends on the slope of the line tangent to the price-yield curve. The lower the slope, the lower the modified duration. The greater the slope the greater the modified duration.
- If the interest rate increases, the new line tangent to the price-yield curve is flatter, which means that the modified duration is lower, and the interest rate risk is also reduced. And vice versa. If the interest rate decreases, the slope of the new line tangent to the price-yield curve is greater, which means that the modified duration is greater, and the interest rate risk is also greater.
Convexity is another measure of interest rate risk. It makes our calculations more precise. As in the case of duration, there are different ways to calculate convexity. In this lesson, we will learn only one of them.
Approximate Convexity Statistic - Formula
Have a look at the formula for the approximate convexity statistic:
The assumed change in the yield \(\Delta r\) should be the same for \(PV_{+}\) and \(PV_{-}\).
Imagine that we purchased a bond with 10 years until maturity. The annual coupon equals 7% and the bond price and par value are equal to USD 100. What is the value of the convexity?
(...)
Now, we will see how to use the convexity adjustment to quantify the interest rate risk. Earlier in the lesson, we used the following formula to compute the percentage change in the bond price:
The percentage change of the bond price equals (-1) times modified duration times yield change.
Now we will upgrade the formula and add the convexity adjustment to it. Have a look:
The percentage change of the bond price equals (-1) times modified duration times yield change plus convexity adjustment.
Convexity adjustment equals 0.5 times convexity times yield change squared.
(...)
We purchased a bond with 10 years until maturity. The annual coupon is 7% and both the bond price and the par value equal USD 100. The convexity equals 64.933 and the modified duration equals 7.0236. What will be the value of the bond price if the yield increases by 45 basis points?
(...)
- Duration measures price sensitivity to changes in interest rates.
- The Macaulay duration can be interpreted as the number of years that an investor has to wait until the investment pays back assuming that the yield doesn’t change and a measure of the interest rate risk.
- We can use the modified duration to compute the percentage price change for a bond assuming a change in the yield.
- The bond price moves in the direction opposite to that of the yield, namely if the yield increases, the bond price will decrease, and if the yield decreases, the bond price will increase
- The greater the modified duration, the greater the percentage price change.
- The greater the yield change, the greater the percentage price change, and the lower the yield change, the lower the percentage price change.
- The duration differs for bonds with different coupons.
- A zero-coupon bond has the Macaulay duration equal to its time to maturity.
- The duration changes in time.
- Convexity is another measure of interest rate risk. It makes our calculations more precise.
- For bonds without embedded options, convexity is always positive.
- If we are to choose between two identical bonds that differ only with respect to convexity, we should always choose the bond with the greater convexity.


