Level 1 CFA® Exam:
Options - Payoff, Moneyness, Value
Payoff
Whatever the underlying asset, the payoff on call options and put options is calculated in a similar way. At expiration, the long party to a call option receives positive payoff if the current market price of the underlying is higher than the exercise price agreed on in the contract. The holder of a put option, in turn, receives a payoff if the current market price of the underlying is lower than the exercise price agreed on in the contract.
The final amount of the payoff is determined based on the number of contracts. Additionally, for each underlying, its value needs to be expressed in monetary units. For this reason, in the case of stock index options, a multiplier is additionally used to determine the dollar value of one index point.
The MAX function selects the higher of the two numbers. Solve:
- MAX(0,3)=?
- MAX(-5,-2)=?
- MAX(-3,2)=?
- MAX(-4,0)=?
- MAX(0,-7)=?
- MAX(0,3)=3
- MAX(-5,-2)=-2
- MAX(-3,2)=2
- MAX(-4,0)=0
- MAX(0,-7)=0
So, the payoff to the long party, regardless of whether it holds a call or a put, is always equal to or greater than zero.
Note: Equivalent American and European options have the same value at expiration.
Moneyness
On the basis of moneyness criterion we distinguish between options that are either profitable or unprofitable to exercise at a given moment. There are 3 types of such options:
- in-the-money options,
- out-of-the-money options, and
- at-the-money options.
(...)
Assume that three months ago you bought a call option on a stock of Company Y. At that time, the price of the stock was USD 60 and the exercise price of the option was USD 65. At present, the stock is trading at USD 70. Is this call option in-the-money, out-of-the-money, or at-the-money?
(...)
Assume that three months ago you bought a put option on a stock of Company Y. At that time, the share price was USD 60 and the exercise price of the option was USD 65. At present, the stock is trading at USD 70. Is this put option in-the-money, out-of-the-money, or at-the-money?
(...)
In terms of moneyness, how would you describe a call option on a stock if you know that:
- the exercise price of the option is USD 105 and the share costs USD 105?
- the exercise price of the option is USD 115 and the share costs USD 105?
(...)
In terms of moneyness, how would you describe a put option on a stock if you know that:
- the exercise price of the option is USD 77 and the share costs USD 70?
- the exercise price of the option is USD 77 and the share costs USD 77?
(...)
Let's consider now whether an option that at a particular time is out-of-the-money has any value at all.
The answer is: yes, it does. If an option is out-of-the-money at a particular time it just means it does not pay to exercise it at that particular time. It does not mean, however, that it cannot become in-the-money and be profitable in the future. The value related to the fact that an option may be more profitable in the future than today is called time value.
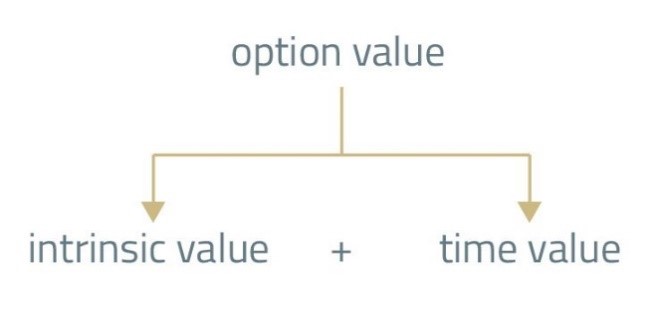
The value of an option is made up of two components: its intrinsic value and its time value.
If S is the spot price of the underlying and X is the option exercise price, the intrinsic value of an option at time ‘t’ is defined as follows:
Intrinsic value is the amount which the holder receives if she decides to exercise an option. If an option is out-of-the-money or at-the-money, the option's intrinsic value is zero.
IMPORTANT: the intrinsic value can be either zero or positive. It cannot take a negative value.
Time value (aka. speculative value) is the amount by which the option premium exceeds the intrinsic value of an option. It represents the amount that an investor is ready to pay hoping that before expiration the value of an option will increase as a result of a beneficial change in the price of the underlying.
The more time left to expiration, the greater the time value of an option. This is a simple consequence of the fact that the longer the period of time is, the greater the likelihood that the situation on the market will turn more beneficial for the option holder becomes. At expiration, the time value of an option is always zero as no more time is left and the option expires.
Based on the data in the table below determine the time value of the following options:
| Option Number | Type of Option | Price of Underlying Asset (S) | Option Exercise Price (X) | Option Price (premium) |
|---|---|---|---|---|
| 1 | call | 34 | 32 | 11 |
| 2 | put | 56 | 67 | 14 |
| 3 | call | 74 | 78 | 5 |
To determine the time value of an option, we first need to determine its intrinsic value:
The intrinsic value of Option 1 (call) equals:
The intrinsic value of Option 2 (put) equals:
The intrinsic value of Option 3 (call) equals:
Since: time value + intrinsic value = option price
Then: time value = option price - intrinsic value
Therefore:
\(\text{Option 1 time value}=11-2=9\)
\(\text{Option 2 time value}=14-11=3\)
\(\text{Option 3 time value}=5-0=5\)
- At expiration, the long party to a call option receives positive payoff if the current market price of the underlying is higher than the exercise price agreed on in the contract. The holder of a put option, in turn, receives a payoff if the current market price of the underlying is lower than the exercise price agreed on in the contract.
- The payoff to the long party, regardless of whether it holds a call or a put, is always equal to or greater than zero.
- Equivalent American and European options have the same value at expiration.
- The value related to the fact that an option may be more profitable in the future than today is called time value.
- Time value (aka. speculative value) is the amount by which the option premium exceeds the intrinsic value of an option.


