Level 1 CFA® Exam:
Market Rate of Return & YTM
In this lesson, we will discuss bond valuation using the market rate of return and we will show how to calculate yield to maturity.
Yield to maturity (YTM) is the annual rate that a bondholder will earn if he or she decides to hold the bond until maturity, assuming the issuer will pay all his obligations in time. The yield to maturity is like the internal rate of return (IRR) that we talked about in the lessons on Corporate Issuers.
We will say how to determine the price of a bond and the yield to maturity using:
- our knowledge about annuities from the Quantitative Methods topic,
- TVM worksheet,
- Bond worksheet, or
- Cash Flow worksheet.
We will also analyze the impact of bond features, such as time to maturity and the value of coupons, on the bond price and the sensitivity of the bond price to changes in the market discount rate.
First, let’s discuss how to value bonds when the coupon has just been paid, that is at the coupon date. Then, we will recall what accrued interest is and how we define flat and full prices.
We start with a bond that is the easiest to value, that is a zero-coupon bond. As you know, these types of bonds don’t pay coupons. An issuer of a zero-coupon bond is obliged to pay only the bond’s par value at a specific time in the future, while investors may earn profits from such a bond because its price is lower than its par value. To value the zero-coupon bond, we have to solve the following equation:
\(PV=\frac{FV}{(1+r)^n}\)
Price (\(PV\)) equals par value (\(FV\)) divided by 1 plus market discount rate (\(r\)) raised to the power of \(n\), where \(n\) stands for the number of periods to maturity.
If an exam question assumes annual compounding, \(n\) is equal to the number of years to maturity. If the question assumes semiannual compounding, \(n\) is equal to the number of years to maturity times two, and so on.
What is the value of a zero-coupon bond with a par value of USD 100 that matures in seven years assuming that the market discount rate equals 12% and the rate is compounded:
- annually?
- semiannually?
What would be the price of this bond if we assumed annual compounding?
\(PV_a=\frac{FV}{(1+r)^n}=\frac{100}{1.12^7}=45.2349\)
What would be the price of this bond if we assumed semiannual compounding?
Firstly, we have to calculate the semiannual interest rate. It is equal to 12% divided by 2 and amounts to 6%. So, the bond price equals:
\(PV_{sa}=\frac{FV}{(1+r)^n}=\frac{100}{1.06^{14}}=44.2301\)
As we can see, all else equal, the more frequent the compounding, the lower the price of the bond.
Let us now turn to a coupon bond. A bondholder of a coupon bond receives not only the payment of the par value (like in the case of a zero-coupon bond) but also coupons, that is payments that occur at regular intervals. The formula presented below is used to value a coupon bond with fixed coupons:
It is 1 January 2022. Stark, Inc. is issuing today a 9-year bond with a par value of USD 1,000 and coupons paid on an annual basis that amount to 6% of the par value. The market discount rate is equal to 8%. What is the price of the bond?
Let’s solve this example using 4 methods:
- formulas for the present value of an annuity and the present value of a single cash flow,
- CF and NPV worksheet,
- TVM worksheet, and
- BOND worksheet.
(...)
It is 1 January 2022. Stark, Inc. is today issuing a 9-year bond with a par value of USD 1,000 and coupons paid semiannually that amount to 6% of the par value. The market discount rate is equal to 8%. What is the price of the bond?
(...)
Now let’s see how to compute the bond price if we are at some point in time between coupon payments. First, we will recall three terms, namely:
- accrued interest,
- flat price, and
- full price.
Accrued interest is the interest earned but not yet paid.
Flat price (aka. clean price) is the price of a bond without accrued interest.
Full price (aka. dirty price) is the price that is actually paid for the bond.
Below are the formulas that we use to calculate the full price between coupon dates:
In these formulas, \(t\) stands for the number of days from the last coupon date, and \(T\) stands for the number of days in the coupon period.
As you can see, the formula for accrued interest doesn’t take into account the time value of money. On the other hand, the formula for the full price does take it into consideration. For these reasons, the clean price is usually slightly lower than it should theoretically be.
However, because it is the full price (and not the clean price) that is paid, the simplification used here while computing the accrued interest doesn’t matter both for the buyer and the seller of the bond.
As we said before, there are two main day-count conventions:
- Act/Act, and
- 30/360
The Act/Act day count convention means that we take the actual number of days in a year and the actual number of days in a month. The 30/360 day-count convention assumes that there are 360 days in one year and 30 days in every month.
Depending on which convention we will use, we will have to input different values for \(t\) and \(T\).
On 1 January 2014 Stark, Inc. issued a 9-year bond with a par value of USD 1,000 and coupons paid on an annual basis that amount to 6% of the par value. What will be the full price of the bond on 18 September 2016 assuming that the required rate of return will be equal to 8%?
(...)
Relationship Between Bond Price, Coupons, Market Discount Rate & Time to Maturity
star content check off when doneBond Price vs Coupons
As you probably remember the price of a bond may be:
- higher than the par value. Then, we say that the bond sells at a premium.
- lower than the par value. Then, we say that the bond sells at a discount.
- equal to the par value – we say the bond sells at par.
The price of the bond with fixed coupons:
- equals the par value if the coupon rate is equal to the market discount rate.
- is lower than the par value if the coupon rate is lower than the market discount rate.
- is greater than the par value if the coupon rate is greater than the market discount rate.
If the coupon rate is equal to the market discount rate, then the bondholder’s profit is generated only from the coupons and so the bond’s price has to be equal to par value.
If the coupon rate is lower than the market discount rate, then the total profit of the bondholder is the result of coupons and the difference between the par value and the bond’s price. All else equal, the greater the difference between the market discount rate and the coupon rate, the greater the difference between the par value and the price of the bond.
Finally, if the coupon rate is greater than the market discount rate, then the bond price is greater than the par value. Because the total profit is lower than the value of coupons, the bond price has to be above par value. All else equal, the greater the difference between the coupon rate and the market discount rate the higher the price of the bond.
(...)
The price of the bond is also affected by the term to maturity. Have a look at the graphs. The price of the bond that is at a premium or at a discount, approaches the par value as the maturity date gets closer. In the graphs, you can see the so-called constant-yield price trajectory:
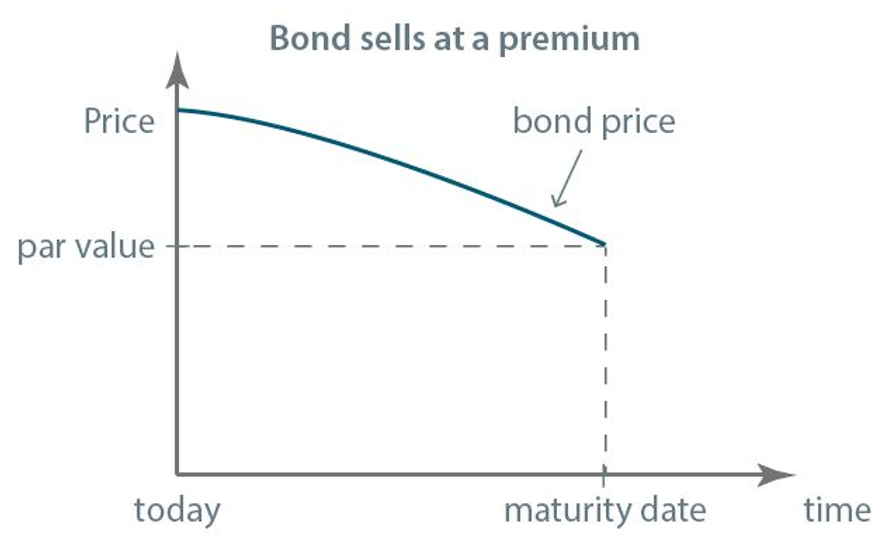
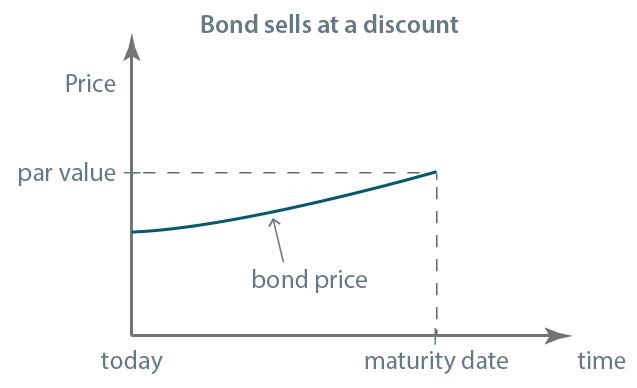
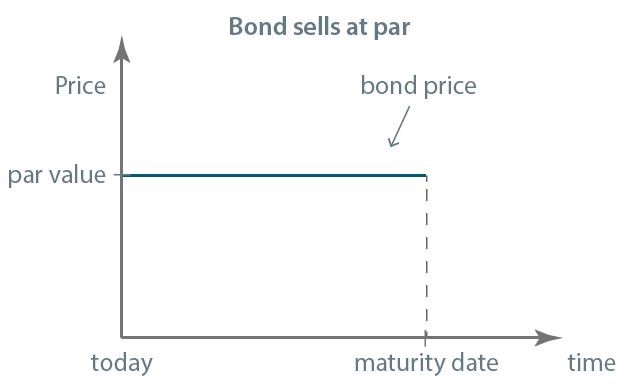
Note that if the market is efficient and if there is a bond with a short term to maturity for which we have reasonable assurance that all commitments will be met, it is unlikely that its price will largely differ from the principal value. So, the price of a bond whose maturity date is close, is close to the par value.
Factors Affecting Sensitivity of Prices to Changes in Interest Rates
star content check off when doneWe’ve already said that the price of the bond is driven by changes in the market discount rate.
Question: Is the percentage change in the bond price the same for all bonds if the change in the discount yield is the same?
For example assume that we have two different bonds X and Y, for which market discount rates are equal to 5%. If the required yields increase by 50 basis points for both bonds, will the percentage change in the price of bond X be the same as the percentage change in the price of bond Y?
The answer to this question is NO.
The sensitivity of the bond price to changes in interest rates is affected by:
- the value of coupons,
- the frequency of coupons payments,
- the time to maturity.
All else equal, the greater the coupons, the lower the sensitivity of the bond’s price to changes in the market discount rate, and vice versa. The lower the coupon rate, the greater the sensitivity of the bond’s price to changes in the market discount rate. All things being equal, zero-coupon bonds are characterized by the greatest sensitivity of the bond’s price to changes in the market discount rate.
All else equal, the more frequently coupons are paid, the lower the sensitivity of the bond’s price to changes in the market discount rate and vice versa. The less frequently coupons are paid, the greater the sensitivity of the bond’s price to changes in the market discount rate.
All things being equal, usually the longer the time to maturity, the greater the sensitivity of the bond’s price to changes in the market discount rate and vice versa. The shorter the time to maturity, the lower the sensitivity of the bond’s price to changes in the market discount rate.
Look at the table presenting 4 different option-free coupon bonds:
| coupon rate | time to maturity | |
|---|---|---|
| Bond A | 6% | 1 year |
| Bond B | 6% | 2 years |
| Bond C | 0% | 5 years |
| Bond D | 4% | 5 years |
Which of these bonds is characterized by the greatest sensitivity of the price to the change in the required yield?
We should take into consideration only the bonds with five years to maturity. Why? Because the longer the maturity, the greater the sensitivity of the bond price. What is more, bonds A and B have also the greatest coupon payments, so they are less sensitive to change in the market discount rate than bonds C and D. Both Bond C and Bond D have five years to maturity but Bond C is a zero-coupon bond and Bond D pays the coupon of 4%. The price of the zero-coupon bond is the most sensitive to changes in the required rate of return from all bonds with the same maturity.
And by the way, what do you think, which of the four bonds has the lowest sensitivity of the price to the change in the interest rate?
Of course, we should choose between Bond A and Bond B. Because they have the same coupon rate and Bond A has only one year to maturity, and Bond B has two years, the price of Bond A is the least sensitive to the change in the market discount rate.
- Yield to maturity is the annual rate that a bondholder will earn if he or she decides to hold the bond until maturity, assuming the issuer will pay all his obligations in time.
- In your level 1 exam you can solve problems related to the price of a bond or yield to maturity using: 1) formulas for the present value of an annuity and the present value of a single cash flow, 2) CF, NPV, and IRR worksheets, 3) TVM worksheet, and 4) BOND worksheet.
- Accrued interest is the interest earned but not yet paid.
- Flat price (aka. clean price) is the price of a bond without accrued interest.
- Full price (aka. dirty price) is the price that is actually paid for the bond.
- The price of the bond with fixed coupons: 1) equals the par value if the coupon rate is equal to the market discount rate, 2) is lower than the par value if the coupon rate is lower than the market discount rate, 3) is greater than the par value if the coupon rate is greater than the market discount rate.
- We have an inverse and convex relationship between the market discount rate and the bond price.
- The price of the bond that is at a premium or at a discount, approaches the par value as the maturity date gets closer.
- All things being equal, zero-coupon bonds are characterized by the greatest sensitivity of the bond’s price to changes in the market discount rate.


