Level 1 CFA® Exam:
Skewness & Kurtosis

Last updated: July 13, 2022

Defining Skewness for Level 1 CFA Exam

   star content check off when done

Skewness is a measure of the asymmetry of a distribution. It tells us how observations are distributed around the mean.

If most observations lie to the left of the mean, we say that the distribution is skewed to the right, or positively skewed. This kind of distribution has a long tail on its right side. When most observations lie to the right of the mean, we say that the distribution is skewed to the left, or negatively skewed. A distribution with a negative skew has a long tail on its left side. Sample skewness is calculated using the formula:

  star content check off when done
Sample Skewness
Click to show formula

\(S_k=\Bigl[\frac{n}{(n-1)\times (n-2)}\Bigr]\times \frac{\sum_{i=1}^n(X_i-\bar{X})^3}{s^3}\)

  • \(S_k\) - sample skewness
  • n - number of observations in a sample
  • \(\bar{X}\) - sample mean
  • \(X_i\) - i observation value
  • s - sample standard deviation

Add note

When S is greater than 0 we're dealing with a positive skew. On the other hand, when S is less than 0, we're dealing with a negative skew.

Note: The above formula is not required to know in your CFA exam.

During the exam, it is important to know what the relationship among the mean, the median, and the mode is if we're dealing with a skewed distribution, irrespective of whether it's skewed to the right or to the left.

When the distribution is symmetrical and unimodal (for example in the case of a normal distribution), the observations are evenly distributed around the mean and the following equation holds:

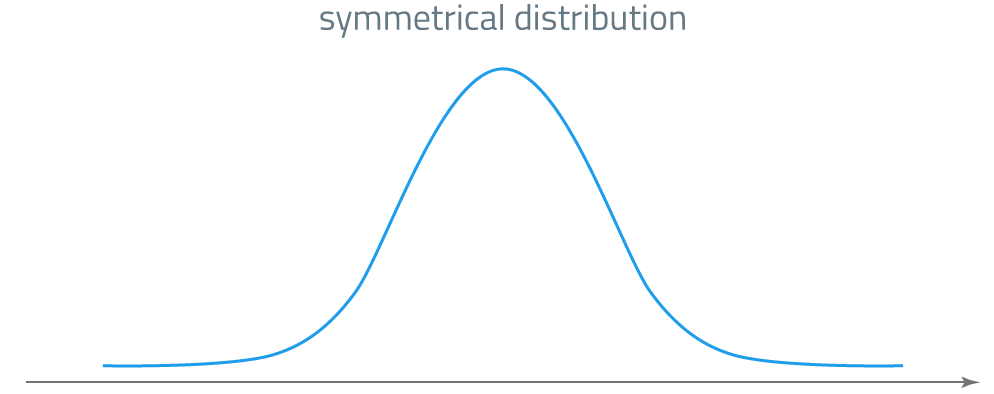
Level 1 CFA Exam: Symmetrical Distribution

\(\text{mean = mode = median}\)

In the case of a positively skewed distribution:

Level 1 CFA Exam: Positively Skewed Distribution

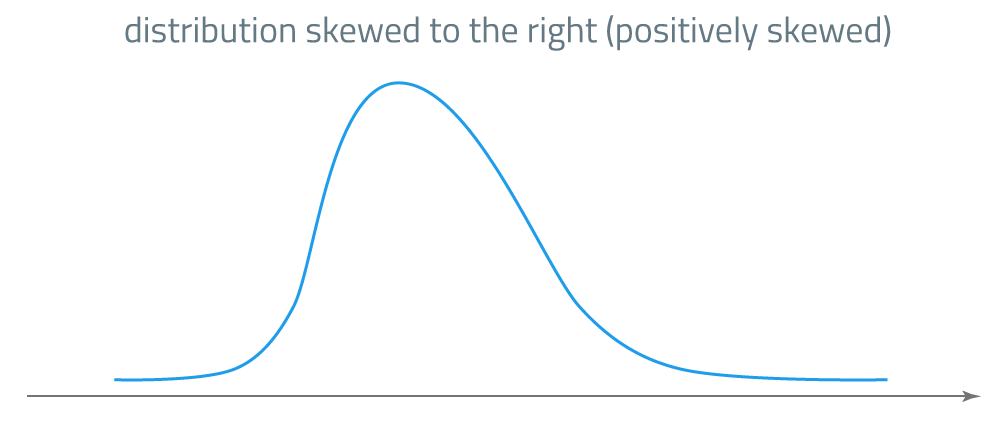
\(\text{mean > median > mode}\)

In the case of negatively skewed distribution:

Level 1 CFA Exam: Negatively Skewed Distribution

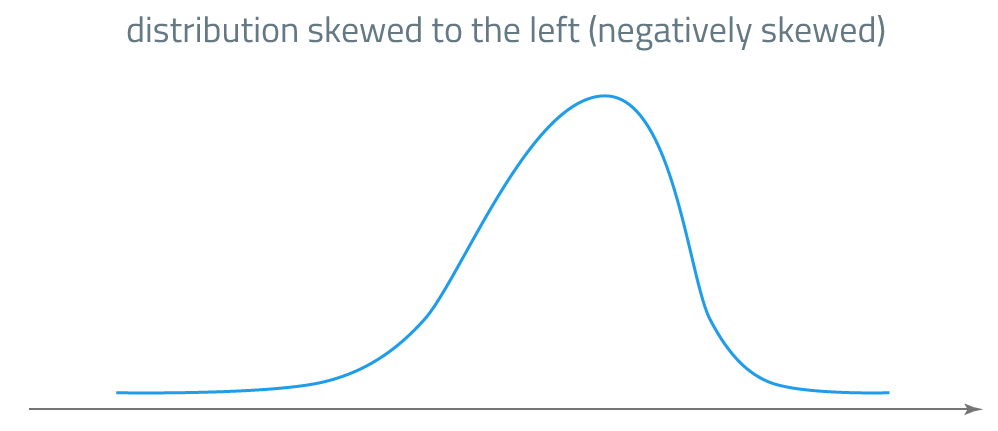
\(\text{mode > median > mean}\)

Note that both for negatively and positively skewed distribution, the median is always between the mode and the mean.

check off when done star content  
Lesson Video

Defining Kurtosis for Level 1 CFA Exam

   star content check off when done

Now let’s move on to kurtosis. Variance can be said to be the second central moment. Skewness is often referred to as the third central moment. The fourth central moment is called kurtosis. Kurtosis is a measure of the peakedness of a distribution or, in other words, a measure of the concentration of results. It tells us how strongly the observations are clustered around the mean.

Based on kurtosis, we can distinguish among 3 types of distribution:

  • leptokurtic,
  • platykurtic, and
  • mesokurtic.

(...)

Create Account Get Full Access

Sample excess kurtosis is expressed as follows:

  star content check off when done
Sample Excess Kurtosis
Click to show formula

\(K_E=\Bigl[\frac{n\times (n+1)}{(n-1)\times (n-2)\times (n-3)}\Bigr]\times \frac{\sum_{i=1}^n(X_i-\bar{X})^4}{s^4}-3\times \frac{(n-1)^2}{(n-2)\times (n-3)}\)

  • \(K_E\) - sample excess kurtosis
  • n - number of observations in a sample
  • \(\bar{X}\) - sample mean
  • \(X_i\) - i observation value
  • s - sample standard deviation<\li>

1) Kurtosis is a measure of the peakedness of a distribution or, in other words, a measure of the concentration of results. It tells us how strongly the observations are clustered around the mean. Types of distribution:

leptokurtic (if observations for a distribution are more concentrated around the mean than in the case of a normal distribution),

platykurtic (when observations are less concentrated around the mean than in the case of a normal distribution),

mesokurtic (when distribution is similar to a normal distribution).

2) A normal distribution has excess kurtosis equal to zero.

Add note

Note: The above formula is not required to know in your CFA exam.

Excess kurtosis is the value by which the kurtosis of a distribution differs from the kurtosis of a normal distribution. Therefore, the excess kurtosis of a normal distribution is zero.

For leptokurtic distributions, excess kurtosis is greater than zero.

The excess kurtosis of platykurtic distributions is less than zero.

check off when done star content  

Level 1 CFA Exam Takeaways: Skewness & Kurtosis

   star content check off when done
  1. Skewness is a measure of the asymmetry of a distribution.
  2. If most observations lie to the left of the mean, we say that the distribution is skewed to the right, or positively skewed.
  3. When most observations lie to the right of the mean, we say that the distribution is skewed to the left, or negatively skewed.
  4. In the case of a positively skewed distribution: mode
  5. In the case of negatively skewed distribution: mode > median > mean.
  6. Kurtosis is a measure of the peakedness of a distribution or, in other words, a measure of the concentration of results.
  7. If observations for a distribution are more concentrated around the mean than in the case of normal distribution, such a distribution is called leptokurtic (fat-tailed).
  8. A distribution is platykurtic (thin-tailed) when observations are less concentrated around the mean than in the case of a normal distribution. # Distributions similar to a normal distribution are called mesokurtic distributions.
  9. Excess kurtosis is the value by which the kurtosis of a distribution differs from the kurtosis of a normal distribution.
check off when done star content