CFA Level 1: NPV & IRR

Introducing NPV & IRR to Level 1 CFA Candidates

star content check off when done

In this lesson, we're going to deal with the evaluation of investment projects. We're going to discuss the most important criteria for evaluating projects, namely the net present value (NPV) and the internal rate of return (IRR).

Net present value is the fundamental measure of investment project profitability. NPV is used to calculate the present value of all cash flows in a project, both negative and positive ones. If the sum of the present values of cash flows is greater than zero, the project is profitable, if it's less than zero, you shouldn't proceed with the project.

Internal rate of return is a discount rate at which NPV equals 0. If the IRR is higher than the required return on the investment, we should invest in the project. If it's lower, we shouldn't.

Net Present Value (NPV) in CFA Exam

star content check off when done

An investment's net present value is the sum of the discounted cash flows of an investment project:

star content check off when done

Net Present Value

Click to show formula

$NPV=\Sigma^{n}_{t=0}\frac{CF_{t}}{(1+r)^{t}}$

$CF_{t}$ - after-tax cash flow at time "t"
$r$ - required rate of return for the investment
$t$ - moment of time

Add note

In exam problems, you are likely to deal with projects in which there's only one negative cash flow at the very beginning of the investment (i.e. at time 0). For projects with a single initial outlay, the net present value equals the present value of future after-tax cash inflows less the initial outlay. This relationship is expressed in the following formula that you’ll surely need in your level 1 CFA exam:

star content check off when done

Net Present Value (with Initial Outlay)

Click to show formula

$NPV=\Sigma^{n}_{t=1}\frac{CF_{t}}{(1+r)^{t}} - CF_{0}$

$CF_{t}$ - after-tax cash flow at time "t"
$r$ - required rate of return for the investment
$CF_{0}$ - investment cash flow at time zero
$t$ - moment of time

Add note

The example below shows how we can use NPV to evaluate a classic investment project with only a single negative cash flow, i.e. the initial outlay at time 0.

star content check off when done

Example 1 (NPV calculation)

A company is considering whether or not to proceed with an investment project that requires an initial outlay of USD 100,000. The after-tax cash inflows are estimated to amount to USD 50,000 at the end of the first and second year and to USD 60,000 at the end of the third and fourth year. The required rate of return for the project is 7%. Compute the NPV of the capital project using formulas AND calculator cash flow worksheet.

show solution

The first step in solving a problem such as this one is to draw a timeline.

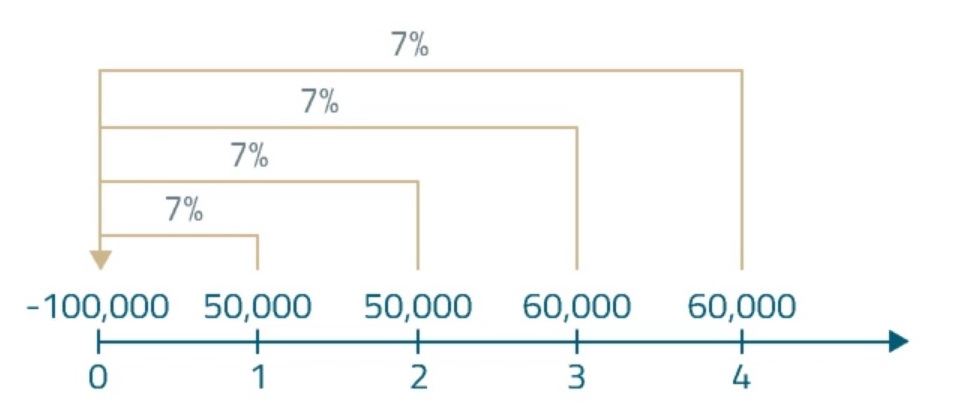
There are four cash inflows happening in consecutive years starting from the end of year one. The first one is USD 50,000 in a year, then we have USD 50,000 in two years, USD 60,000 in three years, and another USD 60,000 at the end of the fourth year. To find out the present value of the inflows, we need to discount the cash inflows at the required rate of return for the project, which equals 7%. Additionally, there's one negative cash flow at time 0 (today), which we don't need to discount as we know its present value.

In the exam, you can calculate the net present value in three ways:

Method 1: using the NPV formula,
Method 2: using the formula, but also a trick to simplify the calculations, or
Method 3: using the cash flow worksheet in the Texas Instruments Professional calculator.

Method 1:

How do we make the calculations directly from the formula, but with the help of such functions of the calculator as the inverse of a number (1/x) and the calculator's memory, with the calculator set in the CHAIN mode rather than AOS?

But what are the modes about? In the CHAIN mode, the user has to remember the order of operations. It's the standard setting in financial calculators. AOS (which stands for Algebraic Operation System) is more typical of scientific calculators. It remembers the order of operations. For example, if you enter:

$2+2\times2$ , the CHAIN mode answer will be 8 (2+2 equals 4 times 2 equals 8), in the AOS mode, you'll get the correct result, that is 6.

So when using the CHAIN mode, you must remember to use parentheses. Our example would have to look like that:

2 [+] [(] 2 [ $\times$ ] 2 [)] [=] 6.

Alternatively, you can change the order of operations. Here you'd have to first do the multiplication and then the addition:

$2\times2+2=6$

Neither mode is better than the other, it's a matter of individual preferences. We're mostly going to use the calculator in the CHAIN mode. To switch between CHAIN mode and AOS mode, press [2nd] [FORMAT] [Arrow UP] and [2nd] [SET] to switch between modes.

Let’s discuss, how to deal with the order of operations if there's exponentiation in the denominator and we have our calculator set in the CHAIN mode.

Let's return to the problem and start with the last flow. We first need to calculate the value of the denominator and then invert it. Then we need to multiply it by the value of the cash flow in a given year, press equality sign, and (STO 4):

1.07 [ $y^x$ ] 4 [=] [1/x] [ $\times$ ] 60,000 [=] 45,773.71 [STO] 4

(...)

Create Account Get Full Access

If a project's NPV is greater than zero, the project will be profitable for the company owners. If NPV is less than zero, the company's value will decrease. So we make the decision based on the following rule:

if the net present value $\text{ > }$ 0 we should invest in the project
if the net present value $\text{ < }$ 0 we should reject the project

Effect of NPV on Value of Company

star content check off when done

A business that invests in profitable projects increases the owners' equity and the value of the company by the amount equal to the NPV. Businesses that invest in unprofitable projects lose their owners' equity and lower their value by the amount of the negative NPV. NPV has a similar effect on stock prices. Projects with a positive NPV increase the price of a stock by an amount equal to the NPV per stock (all other things hold constant), whereas projects with a negative NPV decrease the price by an amount of the NPV per stock.

NPV Profile

star content check off when done

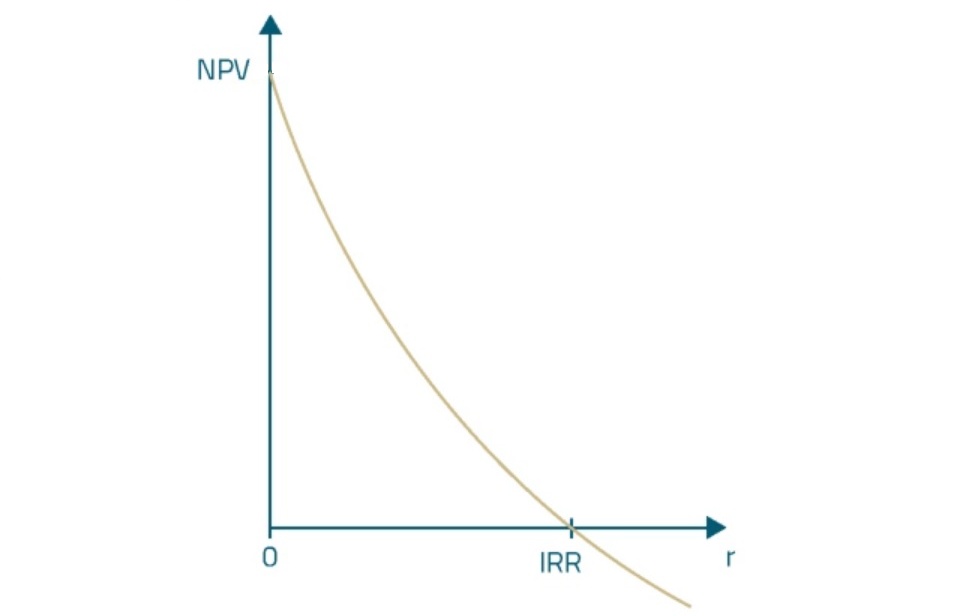
An NPV profile is a graphic representation of the relationship between NPV, measured along the y-axis and the interest rate, measured along the x-axis. Unsurprisingly, the greater the discount rate, the lower the NPV. If the discount rate was 0%, the NPV would equal the sum of undiscounted cash flows in the project. The point where the NPV profile crosses the horizontal axis is the discount rate which we call the internal rate of return.

Internal Rate of Return (IRR) in CFA Exam

star content check off when done

The second very important measure of investment project profitability is the internal rate of return. The internal rate of return is a discount rate at which the present value of future after-tax cash flows equals the initial outlay. In this definition we assume that there's only one initial outlay:

star content check off when done

Internal Rate of Return (with Initial Outlay)

Click to show formula

$\Sigma^{n}_{t=1}\frac{CF_{t}}{(1+IRR)^{t}}-CF_{0}=0$

$CF_{t}$ - after-tax cash flow at time "t"
$IRR$ - internal rate of return
$CF_{0}$ - investment cash flow at time zero
$t$ - moment of time

Add note

We can make the formula more general so that it applies to projects with more than one negative cash flow. This is what it looks like:

star content check off when done

Internal Rate of Return (IRR)

Click to show formula

$0=NPV= \sum_{t=0}^n\frac{CF_t}{(1+IRR)^t}$

IRR - internal rate of return
NPV - net present value
$CF_t$ - net cash flow at time t
n - number of cash flows

1. The internal rate of return is a discount rate at which the NPV of the project is equal to zero.
2. Usually in the questions on the level 1 exam regarding IRR there will an investment (cash outflow) at the beginning of the project and cash inflows in the next periods.
3. To calculate IRR use Cash Flow and IRR sheets on your TiBA II calculator.
4. Regarding project evaluation we should undertake projects for which the IRR is greater than the opportunity cost of capital.
5. For mutually exclusive projects if the NPV rule and the IRR rule choose different projects we should take project with greater NPV.

Add note

Both above equations can be solved only with trial and error or by counting the zeros for n-th degree polynomials, or using a financial calculator. Obviously, in the exam, you're going to use a financial calculator and its IRR worksheet.

A decision whether or not to invest in a project is made like this:

if IRR $\text{ > }$ the required rate of return the company should invest in the project,
if IRR $\text{ < }$ equired rate of return the company should reject the project.

CFA Exam: Multiple IRR Problem & No IRR Problem

star content check off when done

(...)

Create Account Get Full Access

Ranking Conflicts between NPV & IRR

star content check off when done

One very important thing to learn for the exam is the comparison of NPV and IRR.

Generally, when we are dealing with independent projects, there will be no conflict over whether to accept a project or not regardless of the criterion you use. A conflict over which project to choose may, however, occur for mutually exclusive projects. What we mean by conflict here is a situation when the NPV and the IRR suggest two different investment projects, and you need to choose either of the two. If there is such a conflict, you should choose the project with a higher NPV. The reason for that is that NPV gives us a specific value of a project and the higher the value the better for the shareholders.

Level 1 CFA Exam Takeaways: NPV & IRR

star content check off when done

Investment is profitable if NPV is greater than 0.
Investment is profitable if IRR is greater than the cost of the capital involved in financing the investment. If the project financing structure is the same as the company financing structure, the project is profitable if IRR is greater than WACC (weighted average cost of capital).
For mutually exclusive projects we prefer investment A to investment B if $NPV_A > NPV_B$ .
For mutually exclusive projects we prefer investment A to investment B if $IRR_A > IRR_B$ .
The IRR is a relative measure (expressed as a percentage) and, unlike NPV, it doesn't show the absolute value of what we can earn by investing in a project.
In the case of mutually exclusive projects, if there is a ranking conflict between IRR and NPV, we should choose the project with a higher NPV.

Level 1 CFA® Exam: NPV & IRR

Introducing NPV & IRR to Level 1 CFA Candidates

Net Present Value (NPV) in CFA Exam

Effect of NPV on Value of Company

NPV Profile

Internal Rate of Return (IRR) in CFA Exam

CFA Exam: Multiple IRR Problem & No IRR Problem

Ranking Conflicts between NPV & IRR

Level 1 CFA Exam Takeaways: NPV & IRR

Level 1 CFA® Exam:
NPV & IRR