Level 1 CFA® Exam:
Binomial Valuation of Options
In this lesson you’ll learn how the one-period binomial model can be used to value options.
Let’s assume that:
- we have a call option on a stock,
- the price of the call option today is C,
- the price of the stock is S,
- the stock doesn’t pay dividends,
- we assume only one period, and
- there are only two scenarios available for the period: the price of the stock can either increase or decrease.
Our goal is to find out what’s the value of the call option.
Have a look at the graph presenting the two scenarios:
- Scenario 1 assumes that the stock price will increase in the period.
- Scenario 2 assumes that the stock price will decrease in the period.
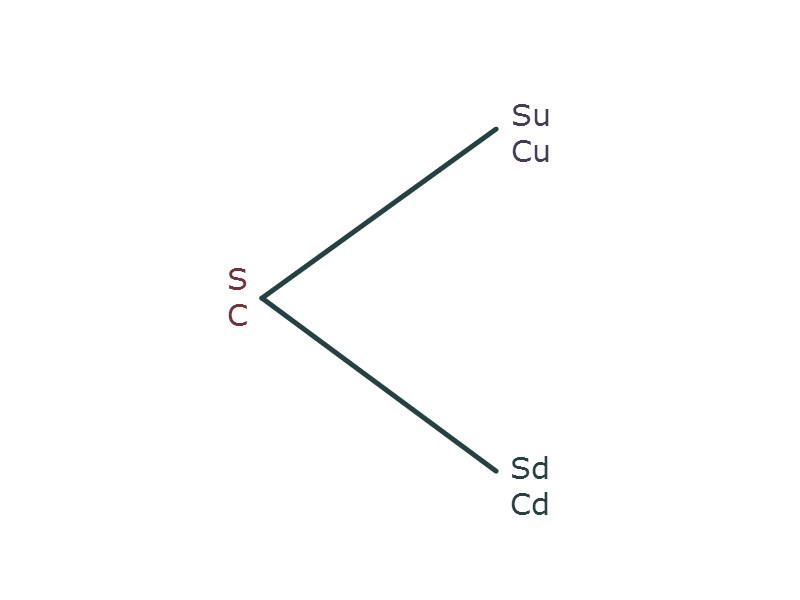
Where:
- S – current price of stock,
- C – current value of call option,
- u – represents an up move in the stock price,
- d – represents a down move in the stock price,
- Su – stock price assuming scenario 1,
- Sd – stock price assuming scenario 2,
- Cu – call option value assuming scenario 1,
- Cd – call option value assuming scenario 2.
To find out what the price of the call option is, we create a risk-free portfolio consisting of call options and stocks. How do we achieve this?
We know that the prices of a call option and a stock are directly related, namely when the stock price increases, the call option premium also increases and vice versa – when the stock price decreases, the call option premium also decreases. Therefore, in the risk-free portfolio we should have call options and stocks in different positions. Thanks to this, changes in the price of one instrument will be offset by changes in the price of the other instrument. There is an infinite number of such risk-free portfolios, and we choose one of them.
We assume that our risk-free portfolio (portfolio F) consists of:
- 1 short call, and
- a number of long positions in a stock. We will refer to the number of long positions in a stock as delta (\(\Delta\)).
\(\text{current value of portfolio F}=\Delta\times{S}–C\)
If the price of the stock increases (scenario 1), then the value of portfolio F will be equal to:
\(\Delta\times{Su}-Cu\)
If the price of the stock decreases (scenario 2), then the value of portfolio F will be equal to:
\(\Delta\times{Sd}-Cd\)
If portfolio F is risk-free, then the value of the portfolio in the upper and lower node should be equal. Why? This results from the definition of a risk-free investment. Regardless of the circumstances and assumed scenarios, the value of the risk-free investment should be the same at the end of a given period.
Therefore:
\(\Delta\times{Su}-Cu=\Delta\times{Sd}-Cd\)
\(\Delta=\frac{Cu-Cd}{Su-Sd}\)
Our conclusion is as follows, if the number of long positions in the stock is \(\frac{Cu-Cd}{Su-Sd}\), portfolio F is a risk-free portfolio.
What is the return on a risk-free investment?
Because the rate of return on a risk-free investment is equal to the risk-free interest rate (r), then:
\((\Delta\times{S}-C)\times(1+r)=\Delta\times{Su}-Cu=\Delta\times{Sd}-Cd\)
If we substitute \(\Delta\) by \(\frac{Cu-Cd}{Su-Sd}\), we will get the following formula for the price of a call option today:
We can say that the price of a call option is equal to the present value of the weighted average of the two values of the call option one period from now, where weights are equal to p and (1-p).
What’s very important here is that exactly the same formula can be applied to put option valuation.
There is a 1-year European call option on a stock with an exercise price of USD 102. The price of the stock today is USD 100 and the annual risk-free interest rate is 5%.
u=1.08, d=0.94
What is the value of the call option today? (use formulas)
1) We begin with calculating \(Su\) and \(Sd\):
\(Su=100\times1.08=108\)
\(Sd=100\times0.94=94\)
2) Now, we can compute \(Cu\) and \(Cd\):
- \(Cu\) is the value of the option if we assume that the price of the stock one year from now is USD 108 (\(Su\)). Because we are dealing with a 1-year option, the value of the option will be equal to its payoff. Because \(Su\) is greater than X, that is the option’s exercise price, the call option payoff equals \(Su-X=108-102=6\). Therefore \(Cu=6\).
- \(Cd\) is the value of the option if we assume that the price of the stock one year from now is equal to USD 94 (\(Sd\)). Because USD 94 is lower than USD 100 (that is the exercise price X), then the call option payoff equals USD 0 and \(Cd=0\).
3) In order to value the call option, we need to calculate the value of \(p\) first:
\(p=\frac{1+r-d}{u-d}=\frac{1+0.05-0.94}{1.08-0.94}=\frac{0.11}{0.14}=0.7857\)
\(1-p=1-0.7857=0.2143\)
4) Finally, the value of the call option is:
\(C=\frac{0.7857\times6+0.2143\times0}{1.05}=4.4898\)
There is a 1-year European call option on a stock with an exercise price of USD 102. The price of the stock today is USD 100 and the annual risk-free interest rate is 5%.
u=1.08, d=0.94
What is the value of the call option today? (use the concept of a risk-free portfolio)
(...)
There is a 1-year European put option on a stock with an exercise price of USD 102. The price of the stock today is USD 100 and the annual risk-free interest rate is 5%.
u=1.08, d=0.94
What is the value of the put option today? (use formulas)
(...)
Important: We can easily check whether our calculations are correct using put-call parity. According to put-call parity, the price of a put option is equal to:
\(P=C+\frac{X}{1+r}-S=4.4898+\frac{102}{1.05}-100=1.6327\)
So we get exactly the same value as in Example 3.
- In binomial valuation of call options we assume that our risk-free portfolio consists of 1 short call, and a number of long positions in a stock. We will refer to the number of long positions in a stock as delta (\(\Delta\)).
- Regardless of the circumstances and assumed scenarios, the value of the risk-free investment should be the same at the end of a given period.
- In binomial valuation when computing the call value using formulas we begin with calculating stock price in the upper and bottom nodes. Then we compute the call payoff for each scenario. Then we need to calculate the value of risk-neutral probabilities. Finally we compute the call value today as equal to the present value of the weighted average of the two values of the call option one period from now, where weights are equal to risk-neutral probabilities.
- Risk-neutral probabilities are the probabilities that would exist if we assumed that investors are risk-neutral.


