Level 1 CFA® Exam:
Lognormal Distribution

Last updated: July 15, 2022

Lognormal Distribution in CFA Exam: Definition, Properties, Formulas

   star content check off when done

In one of the previous lessons, we discussed the normal distribution. Another distribution that is widely used in finance is the lognormal distribution. It’s used, among others, in the Black-Scholes-Merton option pricing model. So, let’s explain how this distribution is constructed.

If X is a random variable that follows a normal distribution, then \(e^X\) is a random variable that follows a lognormal distribution. \(e\) stands for Euler’s number named after Leonhard Euler – a Swiss mathematician. \(e\) is approximately equal to 2.718.

On the other hand, when X is a random variable following a lognormal distribution, then \(lnX\) is a normally distributed random variable. The natural logarithm (\(ln\)) is the logarithm to the base \(e\).

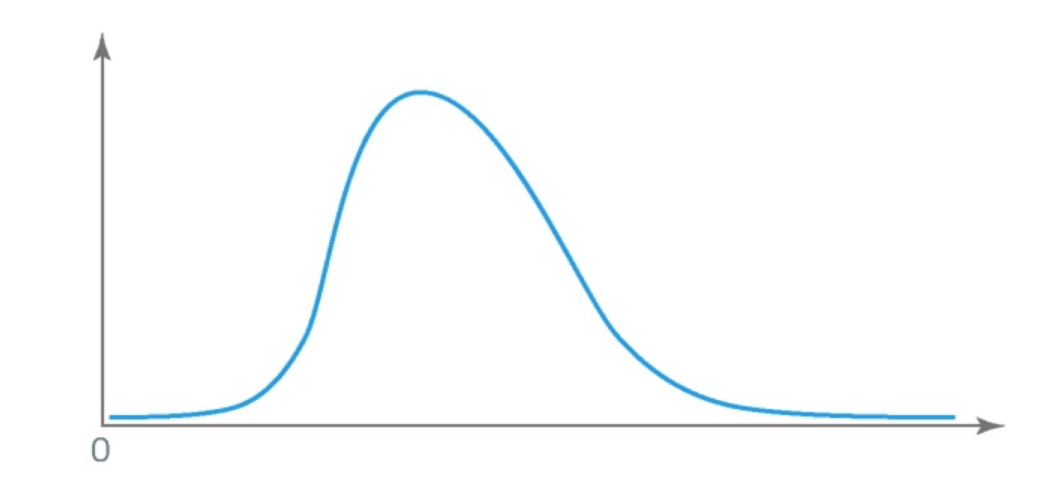
The lognormal distribution has the following properties:

  1. It is skewed to the right.
  2. On the left, it is bounded by 0.
  3. It is described by two parameters of associated normal distribution, namely the mean and variance.
Lognormal Distribution

(...)

Create Account Get Full Access
  star content check off when done
Example 1 (mean and variance of lognormal random variable)

A random variable X is normally distributed with the mean equal to 10% and the standard deviation equal to 25%. What is the mean and variance of the associated lognormal random variable?

A random variable X is normally distributed with the mean equal to 10% and the standard deviation equal to 25%. What is the mean and variance of the associated lognormal random variable?

To calculate the mean of the lognormal random variable, we have to find the variance of the normally distributed random variable first.

The variance equals the standard deviation squared, that is 25% squared, which gives us 0.0625.

So, the mean of the lognormal random variable equals:

\(\text{mean}=e^{0.1+0.5\times0.0625}=1.1403\)

The variance of the lognormal distribution is:

\(\text{variance}=e^{2\times\mu+\sigma^2}\times{(e^{\sigma^2}-1)}= e^{2\times0.1+0.0625}\times{(e^{0.0625}-1)}=0.0839\)

check off when done star content  

Continuously Compounded Returns for Level 1 CFA Candidates

   star content check off when done

Here are 3 formulas for continuously compounded returns that you can use in your level 1 CFA exam:

  star content check off when done
Continuously Compounded Return ('1' Holding Period)
Click to show formula

\(r_{t,t+1} = ln(\frac{S_{t+1}}{S_{t}}) = ln(1+R_{t,t+1})\)

  • \(S_{t}\) - stock price at time "t"
  • \(S_{t+1}\) - stock price at time "t+1"
  • \(R_{t,t+1}\) - holding period return for "t" to "t+1" period
  • \(r_{t,t+1}\) - continuously compounded return for "t" to "t+1" period
Add note
  star content check off when done
Continuously Compounded Return ('T' Holding Periods)
Click to show formula

\(r_{0,T} = r_{T-1,T} + r_{T-2,T-1} + \ldots r_{0,1}\)

  • \(r\) - continuously compounded return
  • \(T\) - investment horizon
Add note
  star content check off when done
Variance ('T' Holding Periods; Continuously Compounded Return)
Click to show formula

\(\sigma^{2}(r_{0,T}) = \sigma^{2}\times T\)

  • \(\sigma^{2}(r_{0,T})\) - variance for T periods
  • \(\sigma^{2}\) - variance for one period
  • assumption: returns are independently and identically distributed (IID)
Add note
  star content check off when done
Example 2 (continuously compounded return)

The price of a stock at the beginning of a year is equal to USD 56 and at the end of the year equals USD 70. What is the holding period return and continuously compounded return for this year?

(...)

Create Account Get Full Access

Very often securities valuation models assume that continuously compounded returns of securities are normally distributed. Based on this assumption, it can be proved that prices of securities are lognormally distributed. Thanks to it, we can use the lognormal distribution to model the probability distribution of security prices, which is very useful for modeling prices of securities.

You should also remember that even if continuously compounded returns of securities are not exactly normally distributed, then according to the central limit theorem, security prices can be well described by the lognormal distribution.

check off when done star content  
Lesson Video

Level 1 CFA Exam Takeaways: Lognormal Distribution

   star content check off when done
  1. If X is a random variable that follows a normal distribution, then \(e^X\) is a random variable that follows a lognormal distribution.
  2. The lognormal distribution has the following properties: (1) It is skewed to the right, (2) on the left, it is bounded by 0, and (3) it is described by two parameters of associated normal distribution, namely the mean and variance.
  3. Lognormal distribution can be used for modeling prices and normal distribution can be used for modeling returns.
check off when done star content