Using Spot Rates & Forward Rates In Your CFA® Exam

This blog post was created as a part of the CFA exam review series to help you in your level 1 exam revision, whether done regularly or shortly before your CFA exam.
Level 1 CFA Exam: Spot Rate vs Forward Rate
The spot rate is the yield-to-maturity on a zero-coupon bond, whereas the forward rate is the interest rate expected in the future. Bond price can be calculated using either spot rates or forward rates.
Definitions
Spot rate (z) is defined as yield-to-maturity on a zero-coupon bond.
If we know more than one spot rate, we can plot a spot curve. The spot curve is a set of yields-to-maturity on zero-coupon bonds with different maturities.
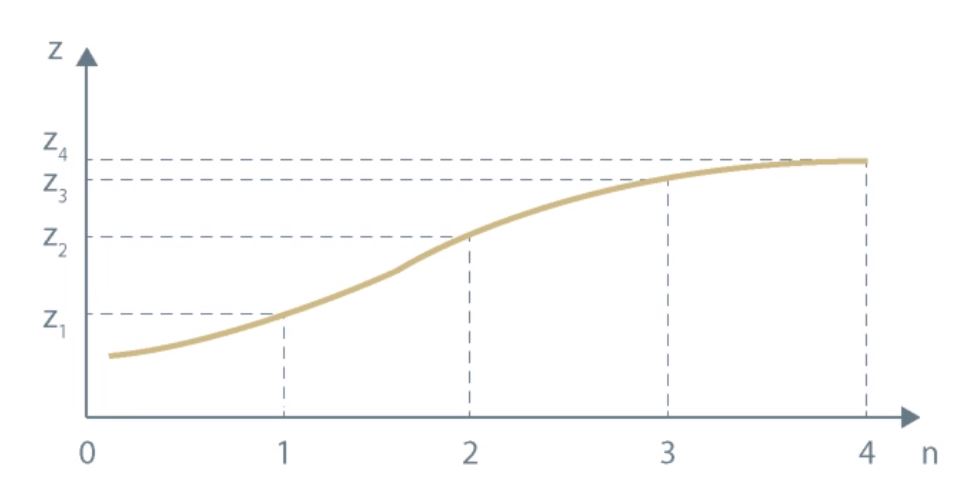
Spot markets are markets for immediate delivery and forward markets are markets for future delivery.
As far as spot markets are concerned, we talk about spot rates. For forward markets, we have forward rates (f). Quite obviously, the former are interest rates on financial instruments traded in spot markets, while the latter are interest rates on financial instruments traded in forward markets.
The forward curve presents different forward rates for different maturities.
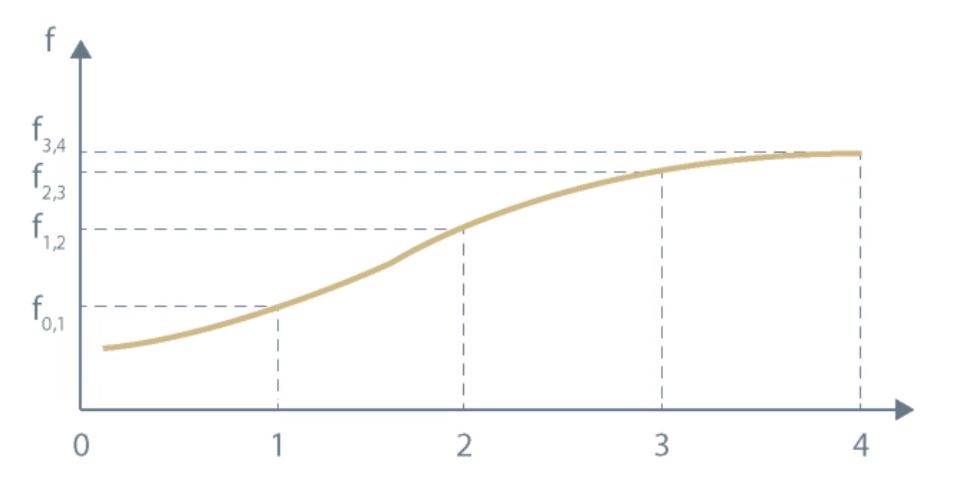
How to Compute a Bond Price Using Spot Rates?
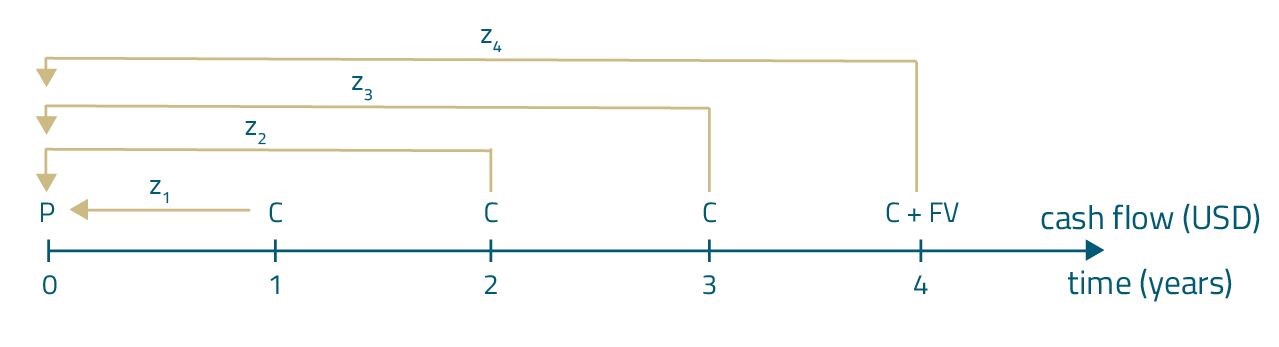
Valuation of a 4-year bond using spot rates:
Where:
- P – bond’s value,
- C – coupon payment,
- FV – par value,
- \(z_1\), \(z_2\), \(z_3\), \(z_4\) – spot rates.
Please note that each cash flow is discounted using a different spot rate:
The table below presents different spot rates:
Year | Spot rate |
1 | 2.2% |
2 | 2.5% |
3 | 3.0% |
4 | 3.2% |
The value of a four-year coupon bond with an annual coupon of USD 4 and a par value equal to USD 100 is closest to:
- USD 98.
- USD 102.
- USD 103.
Answer: C
\(P=\frac{4}{1.022}+\frac{4}{(1.025)^2}+\frac{4}{(1.03)^3}+\frac{104}{(1.032)^4}\)
\(P=3.9139+3.8073+3.6606+91.6884=103.0702\)
Please note that we discounted each coupon (or coupon + par value in the case of Year 4) by a different spot rate from the table.
Note: In the exam, pay attention to the answers! For example, in this question answer A is impossible. That’s because, based on the data given, we would expect the bond to be selling at a premium because all spot rates are lower than the coupon rate. Thus, the value of the bond should be higher than its par value.
How to Compute a Bond Price Using Forward Rates?
Valuation of a 3-year bond using forward rates:
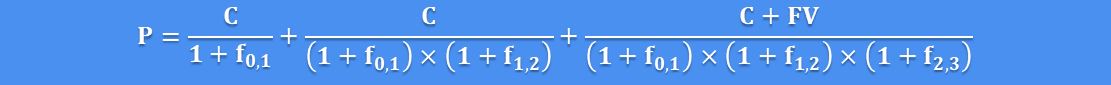
Where:
- P – bond’s value,
- C – coupon payment,
- FV – par value,
- \(f_{2,3}\) – forward rates.
Please note that above we used 1-year forward rates to find the bond price. However, we can also use longer forward rates, e.g. 2-year forward rates.
Pay also attention to forward rates notation:
\(f_{n,n+k}\) means an implied k-year forward yield n years into the future (n-year into k-year rate; nyky; n’s, k’s), e.g.
\(f_{2,5}\) is an implied 3-year forward yield 2 years into the future (2-year into 3-year rate; 2y3y; 2’s, 3’s)
Implied Forward Rate vs Implied Spot Rate
If we know two different spot rates, we can compute the implied forward rate:
\((1+z_n)^n\times(1+f_{n,n+k})^k=(1+z_{n+k})^{n+k}\)
for example:
\((1+z_3)^3\times(1+f_{3,5})^2=(1+z_5)^5\)
Where:
- \(z_n\) is the yield-to-maturity on a zero-coupon bond maturing in n years,
- \(z_{n+k}\) is the yield-to-maturity on a bond maturing in (n+k) years,
- \(f_{n,n+k}\) stands for implied k-year forward yield n years into the future.
Of course, we can rearrange the formulas and make the implied forward rate the subject of the formula. In the case of interest rates stated on an annual basis, the implied forward rate equals:
\(f_{n,n+k}=[\frac{(1+z_{n+k})^{n+k}}{(1+z_n)^n}]^{\frac{1}{k}}-1\)
If we know different forward rates we can compute the implied spot rate, e.g. if we know the \(f_{0,1}\) and \(f_{1,2}\), we can compute the implied \(z_2\):
\((1+f_{0,1})\times{(1+f_{1,2})}=(1+z_2)^2\)
\(z_2=[(1+f_{0,1})\times{(1+f_{1,2})}]^{0.5}-1\)
In a table below, spot rates for different years are given:
Year | Spot rate |
1 | 2.2% |
2 | 2.5% |
3 | 3.0% |
4 | 3.2% |
If we want to compute the implied 2-year into 1-year rate, we should most likely use the following spot rates:
- ...
- ...
- ...
Question 2 is available for CFA exam candidates using our study planner to control their prep:
Already using Soleadea? 1. Sign into your account 2. Refresh this page to see Question 2.
Level 1 CFA Exam Takeaways for Spot Rates and Forward Rates
- The spot rate is the yield-to-maturity on a zero-coupon bond, whereas the forward rate is the rate on a financial instrument traded on the forward market. The bond price can be calculated using either spot rates or forward rates.
- We can calculate the implied forward rate from spot rates and vice versa: we can calculate the implied spot rate from forward rates.
- The implied forward rate can be perceived as the breakeven reinvestment rate.
- Forward rates help us exploit arbitrage opportunities if such opportunities arise.
- The yield curve is a set of yields-to-maturity on coupon bonds with similar credit ratings and different maturities.
- The spot curve is a set of yields-to-maturity on zero-coupon bonds (spot rates) with similar credit ratings and different maturities.
- The forward curve is a set of forward rates for equal periods at different points in time.
- The par curve is a set of yields-to-maturity on coupon bonds priced at par with similar credit ratings and different maturities.
- If consecutive spot rates are higher and higher, then the forward curve is above the spot curve.
- If the spot curve is downward sloping, then the forward curve is below the spot curve.
LAST UPDATE: 2 Nov 2023
Read Also:




